NEW TEMPLATE AVAILABLE - INCLUDING SAMPLE SIZE CALCULATOR!
DOWNLOAD VIA FORM BELOW

Creation Process

1. The Objective

On a daily basis I use a wealth of sample data to try and calculate the answer to a variety of questions. One of these questions is forecasting production and to answer this I need a variety of metrics. To get this, we don't go make 60,000 measurements. Instead, we use a sample of 20.

My theory was that this small sample size wouldn't reflect the population 100% accurately, and my calculation relied on so many sample measures, when you account for all the errors, my production forecast would be too far off.

This was where a confidence interval would come in handy, it would tell me how much my sample would be off with an x% amount of confidence. I could then calculate an upper, and lower forecast limit and predict that the actual production would fall in between. I could then strengthen the argument for my models accuracy, and get more funding to collect a larger sample.

2. Research (the hard part)

I am not a statistician. I did one paper in statistics (which I actually enjoyed) at university, but remember none of it. Luckily excel formulas don't forget, so yet another reason to get an easy to use calculator up and running. I am told statisticians turn their nose up at Excel, but buying a SPSS or equivalent license is very expensive and just about every workplace has Microsoft Office. So I argue Excel is a great way to get started - Udacity offer a handful of basic Statistics courses and they use Google Sheets (which is Google's version of Excel). So I take that as an argument for using Excel. 

Most of my calculations are based on this website, Stat Trek. They have a great step by step process, which is perfect for writing an excel formula.
My main concern is that the calculations are incorrect (despite all my checks debunking this concern; which involved asking around at statistic forums and comparing my results to online calculators - all tests came back positive). However if you are a statistician and it is wrong, or could be better, please comment below or tweet me.

As a result, I will be listing the formulas but not explaining the statistics. View a detailed explanation using the above Stat Trek link.

3. Building The Sheet

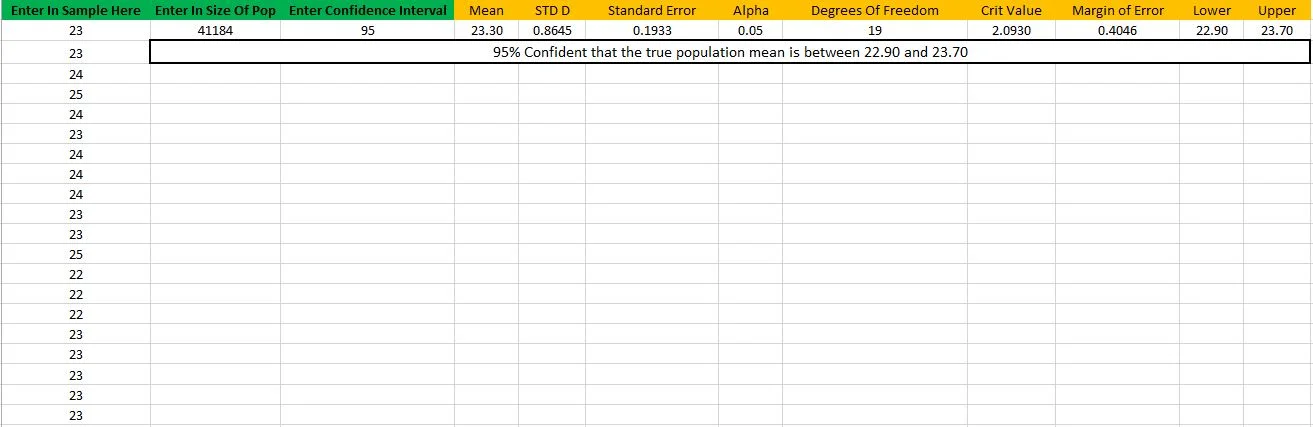
1. Design your layout - I use 11 columns. 2 Green inputs and 9 orange formulas.

2. Enter some data into column A, for example height measurements of people in your department. In column B, enter in how confident you want to be in your interval. 95 is the default.

3. In column C, add in an average formula =AVERAGE(A2:A2100) . In column D, add in a Standard Deviation formula (using the population one here) =STDEV(A2:A2100) .

4. Next we calculate the standard error in column E, =D2/(SQRT(COUNT(A2:A2100))) . This is standard deviation of the sample, divided by the square root of the sample size.

5. Add the alpha to column F, =1-B2/100 . The degrees of freedom goes in column G, =COUNT(A2:A2100)-1 .

6. As opposed to using an online calculator to find the critical value, simply use =TINV(F2,G2) in column H. The margin of error is simply the critical value * the standard error, =H2*E2 this goes in column I.

7. You can now calculate your intervals - in column J =C2-I2 and column K =C2+I2.

8. Merge cells B3:K3. In the merged cell, add this formula: =B2&"% "&" Confident that the true population mean is between "&TEXT(J2,"0.00")&" and "&TEXT(K2,"0.00")

9. You now have a confidence interval calculator!

4. Summary

This calculator is very simple and as a result easy to build. Always use it with a grain of salt, for example if your department was predominately men, the average height would be above that of your population which means the confidence interval would be wrong and not represent the population correctly.

It generates identical results to most online calculators.

Now that you have data you are confident about, why not use it to model a forecast? Follow my Excel Linear Forecast Tutorial!

5. Download (New template with Sample Size Calculator)

More templates